Bienvenid@s a este nuevo artículo que vamos a dedicar a explicar los números decimales para educación primaria. A lo largo del artículo podremos aprender qué es un número decimal, sus principales características, que partes los componen, los tipos que hay, operaciones con números decimales, su relación con las fracciones etc. Además, encontraréis una actividad que podréis probar y que está incluida en nuestra plataforma educativa Smile and Learn, llamada “Decimales”.
La plataforma educativa Smile and Learn cuenta con más de 5.000 recursos didácticos para niñ@s de edades comprendidas entre los 3 a 12 años. En ella pueden trabajar desde el aula o a distancia, las principales materias educativas correspondientes a su edad.
Si deseas probarla puedes solicitar un usuario demo de Smile and Learn durante 30 días totalmente gratis y sin compromiso.
Y ahora vamos a empezar con el primer apartado para conocer “Qué son los números decimales”. Esperamos que os sirva de ayuda.
ÍNDICE DE CONTENIDO
JUEGO PARA APRENDER LOS NÚMEROS DECIMALES
Crea tu usuario demo en Smile and Learn y empieza a jugar con una de nuestras aplicaciones favoritas para aprender los números decimales:
QUÉ SON LOS NÚMEROS DECIMALES
Un número decimal es un número no entero, compuesto por una parte entera y una parte decimal, y se usan cuando queremos representar números que son más pequeños que la unidad.
Por ejemplo, 0,5 es un número decimal, y es más pequeño que la unidad, ya que se cumple que 1 es mayor que 0,5.
A continuación veremos las partes de las que se compone un número decimal.
PARTE ENTERA Y PARTE DECIMAL
Cada número decimal consta de una parte entera y una parte decimal que van separadas de una coma. La parte entera va a la izquierda de la coma, y puede incluir el cero. La parte decimal va a la derecha de la coma.
Por ejemplo, en el número decimal 1,3 la parte entera es 1 y la parte decimal es 3.
CÓMO SE ESCRIBEN LOS NÚMEROS DECIMALES
Los números decimales se escriben usando una coma para separar la parte entera de la parte decimal. Lo más común es encontrarlos usando la coma, pero en otros países se puede escribir usando punto o apóstrofe.
Por ejemplo:
- Usando coma: 1,5
- Usando punto: 1.5
- Usando apóstrofe: 1’5
DÉCIMA, CENTÉSIMA Y MILÉSIMA
Para conocer mejor los números decimales vamos a centrarnos en hablar de cómo está compuesta la parte entera y la parte decimal.
A la izquierda de la coma encontramos la parte entera, que puede constar de derecha a izquierda de la coma de: unidad, decena y centena. Para entenderlo mejor, las unidades son las que ocupan el primer espacio a la izquierda de la coma, seguida de la decena y la centena.
A la derecha de la coma encontramos la parte decimal, que puede constar de izquierda a derecha de: décima, centésima y milésima. Para ayudar a su comprensión, las décimas son las que ocupan el primer espacio a la derecha de la coma, seguida sucesivamente de la centésima, y la milésima.
Centena – Decena – Unidad , Décima – Centésima – Milésima
Vamos a centrarnos en explicar la parte decimal. La parte decimal como se ha comentado anteriormente, está ubicada a la derecha de la coma y puede constar de décimas, centésimas y milésimas.
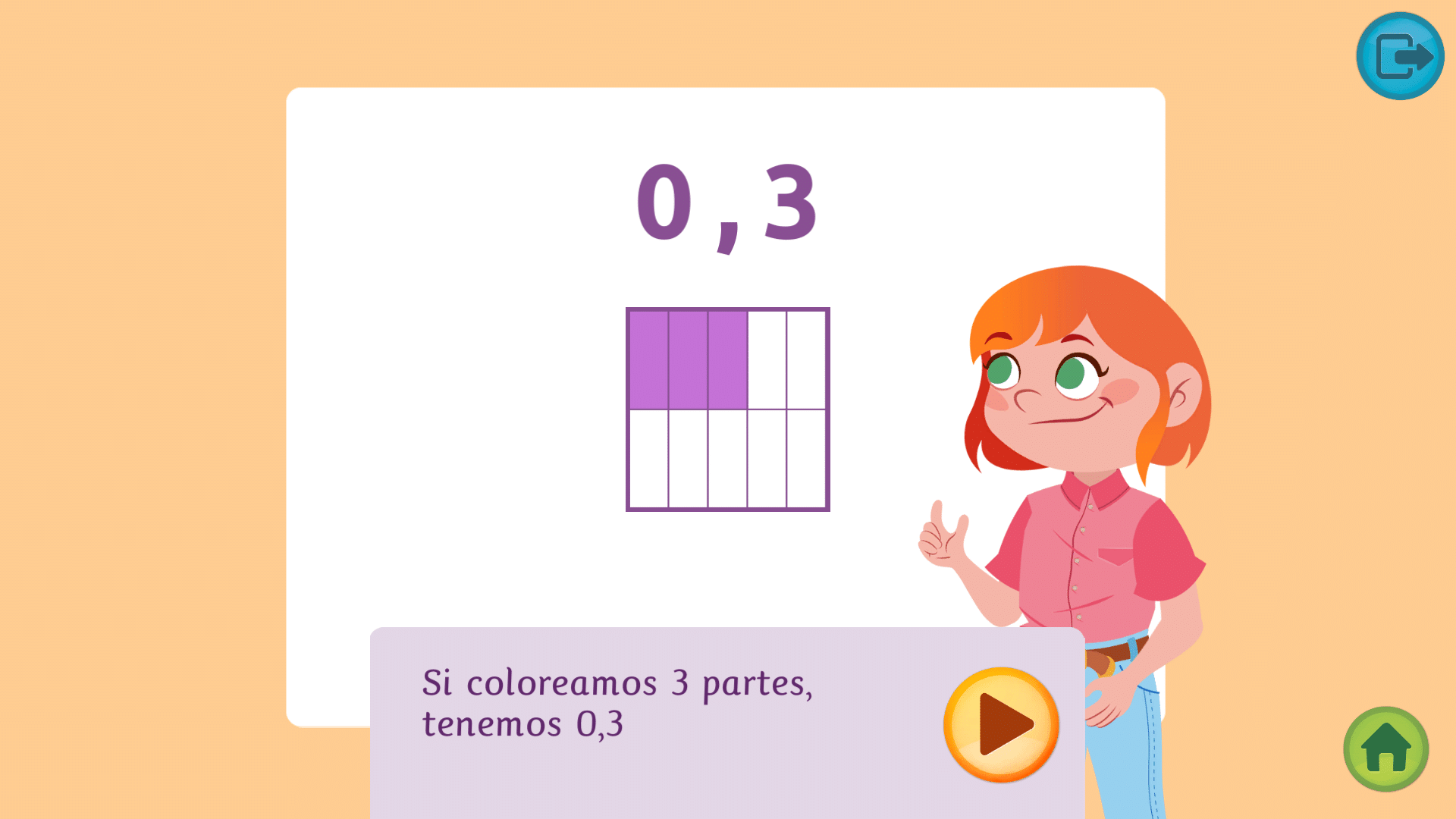
Al dividir en 10 partes iguales el cuadro de la unidad tenemos las décimas. Si coloreamos 3 partes de esas 10, formaremos el número decimal 0,3, que consta de 3 décimas.
Al dividir en 100 partes iguales el cuadrado de la unidad, tenemos las centésimas. Si coloreamos 15 partes, tenemos 0,15, es decir, 15 centésimas.

Y finalmente si se divide en 1000 partes iguales el cuadrado de la unidad, tenemos las milésimas. Por lo tanto, la décima es más pequeña que la unidad. La centésima es más pequeña que la unidad y la décima. Y la milésima es más pequeña que la unidad, la décima y la centésima.
En resumen:
Si dividimos la unidad en 10 partes iguales, tendremos 10 décimas. Si dividimos la unidad en 100 partes iguales, tendremos 100 centésimas. Si dividimos la unidad en 1000 partes iguales, tendremos 1000 milésimas.
LECTURA DE NÚMEROS DECIMALES
Leer números decimales es muy sencillo. La lectura de números decimales se realiza de varias formas. Para verlo, vamos a partir de un ejemplo con el número decimal: 45,68.
- Forma 1: Cuarenta y cinco coma sesenta y ocho.
- Forma 2: Cuarenta y cinco con sesenta y ocho.
- Forma 3: Cuarenta y cinco unidades y sesenta y ocho centésimas.
TIPOS DE NÚMEROS DECIMALES
En este apartado vamos a aprender los tipos de números decimales: decimal exacto, decimal periódico que pueden ser puros o mixtos y decimal no exacto ni periódico.
DECIMAL EXACTO
Los números decimales pueden ser decimal exacto, si están compuestos por un número finito de cifras decimales. Por ejemplo 2,5.
DECIMAL PERIÓDICO
Los números decimales también pueden ser decimal periódico. Son aquellos que tienen una cantidad ilimitada de cifras decimales, es decir, la parte decimal llamada periodo, se repite infinitamente.
Dentro esta clasificación se puede dar que sean periódicos puros o periódicos mixtos.
Los periódicos puros son aquellos que cuentan únicamente con una parte decimal que se repite eternamente. Ejemplo: 0,333333…
Los periódicos mixtos están formados en su parte decimal por una parte no periódica y otra parte que si es periódica. Ejemplo: 0,2566666…
DECIMAL NO EXACTO Y NO PERIÓDICO
Existen números decimales que no pertenecen a ninguno de las clasificaciones anteriores, es decir es un decimal no exacto y no periódico. Por lo tanto, cuentan con infinitas cifras que no se repiten periódicamente. Ejemplo: 3,1534772389…
EJEMPLOS DE NÚMEROS DECIMALES
Para entender mejor la teoría de números decimales vamos a ver a continuación una serie de ejemplos.
El primer ejemplo es con el número decimal 2,5.

Como se puede ver en la imagen, para formar el número decimal 2,5, tenemos coloreados dos cuadrados de unidad y 5 décimas.
Veamos un segundo ejemplo. En este caso tenemos el número decimal 1,25.

En este podemos ver 1 unidad y 25 centésimas coloreadas, esto es 1,25.
Y finalmente, un tercer ejemplo con el número decimal 1,08.

En este ejemplo podemos ver que para formar el número decimal 1,08 compuesto por 1 unidad y 8 centésimas, hay que colorear un cuadrado de unidad y 8 cuadrados de centésimas.
DECIMALES Y FRACCIONES
Los números decimales y las fracciones tienen una gran relación. Una fracción es una parte de un grupo, por ejemplo, la fracción 3/10 nos indica que de una unidad que está dividida en 10 partes iguales, cogemos 3 partes.
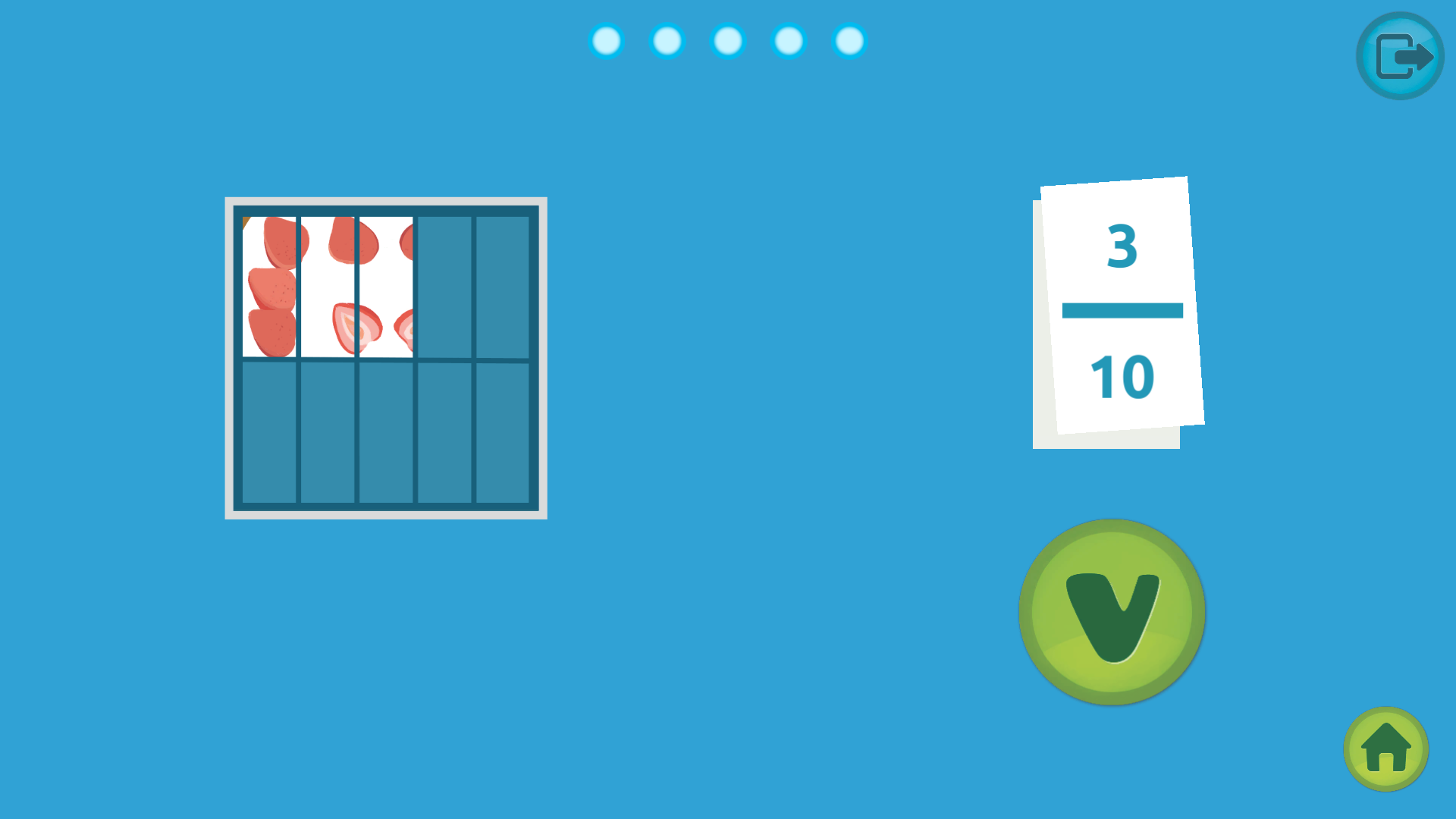
Una fracción está compuesta por diferentes partes. El número que está debajo de la línea es el denominador y nos indica en cuántas partes iguales se divide la unidad. Encima de la línea está el numerador que indica el número de partes que se seleccionan.
Un número decimal, como ya sabemos, está formado por décimas, centésimas y milésimas y la unidad se representa con un 1. Pues con toda esta información, vamos a ver cual es la relación entre números decimales y fracciones.
Al dividir en 10 partes iguales el cuadro de la unidad tenemos las décimas. Si tomamos 1 parte, formaremos el número decimal 0,1 que se corresponde con la fracción 1/10. Ya que, la fracción 1/10 quiere decir que de una unidad que está dividida en 10 partes iguales, tomamos 1. Por lo tanto:
1 décima = 0,1 = 1/10
De igual forma pasa con la centésima y la milésima. Al dividir la unidad en 100 partes iguales y tomamos 1 parte, tendremos el número decimal 0,01, que se corresponde con la fracción 1/100. La fracción 1/100 quiere decir que de una unidad que está dividida en 100 partes iguales, cogemos 1. Por lo tanto:
1 centésima = 0,01 = 1/10
Finalmente, al dividir la unidad en 1000 partes iguales, tendremos las milésimas. Si cogemos 1 parte, formaremos el número decimal 0,001, que se corresponde con la fracción 1/1000. Por lo tanto:
1 milésima = 0,001 = 1/1000
PASAR DE DECIMAL A FRACCIÓN
Una vez que ya sabemos la relación entre números decimales y fracciones vamos a ver como se pasa un decimal a fracción. Para ello, lo más fácil para entenderlo es ver un ejemplo.
Tenemos el número decimal: 2,54
Primero vamos a formar el denominador. Para ello comprobamos cuantas posiciones decimales tenemos ocupadas por números. En este caso el número 5 ocupa el lugar de las decenas y el número 4 ocupa el lugar de las centenas. Por cada uno de ellos deberemos añadir un cero, quedando el denominador como 100. Si hubiésemos tenido el caso en el que solo tuviésemos ocupado el lugar de las decenas, el denominador sería 10.
Una vez que tenemos el denominador, vamos a formar el numerador. El numerador es simplemente el número decimal completo quitando la coma. Por lo que el numerador sería 254. Finalmente, teniendo el numerador y el denominador, solo queda formar la fracción que sería: 254/100.
PASAR DE FRACCIÓN A DECIMAL
Ya hemos aprendido a pasar de decimal a fracción, por lo que solamente quedaría saber como pasar de fracción a decimal. Veamos un ejemplo para entenderlo mejor.
Tenemos la fracción: 65/10
El denominador de la fracción es 10 y el numerador es 65. El numerador nos está indicando cuál es nuestro número decimal. A ese número solo le hace falta la coma correspondiente, para convertirlo en un número decimal. Para conocer el lugar de la coma, es tan sencillo como mirar el denominador. Como el denominador sólo tiene un 0, tendremos que mover la coma a un único lugar, empezando por la derecha. Por lo tanto el número decimal es 6,5.
OPERACIONES CON NÚMEROS DECIMALES
En esta sección vamos a trabajar la suma, resta, multiplicación, comparación y aproximación con números decimales. En Smile and Learn estamos trabajando en nuevas actividades que incluyan operaciones con números decimales. De momento, os dejamos con la teoría y ejemplos.
SUMA
La primera de las operaciones con números decimales que vamos a aprender es la suma. La suma de números decimales se realiza de igual forma que cualquier suma, pero con la diferencia que hay que tener en cuenta la coma al terminar. Para ello se colocan los números decimales en columnas, en el que se hagan coincidir la parte entera con la parte entera, la coma con la coma y la parte decimal con la parte decimal.
Se realiza como cualquier suma, solo con la diferencia que colocaremos la coma en la misma posición en la que estaba. A continuación tenéis un ejemplo en el que podréis ver visualmente como se realiza, para entenderlo mejor.

Si sumamos los números decimales 125,321 y 35,1 el resultado que obtenemos es 160,421. Como podemos comprobar, la suma se hace igual, simplemente que hay que colocar la coma en la posición que tiene.
RESTA
La resta de números decimales se realiza igual que hemos explicado en el apartado anterior con el caso de la suma de decimales. Se colocan los números decimales en columnas, en el que se hagan coincidir la parte entera con la parte entera, la coma con la coma y la parte decimal con la parte decimal.
Se realiza como en cualquier resta, colocando la coma en el lugar que ocupa. Os ponemos un ejemplo a continuación. 
Si restamos los números decimales 48,8 y 33,1 el resultado que obtenemos es 15,7. Como podemos comprobar, la resta se hace igual, simplemente que hay que colocar la coma en la posición que tiene.
MULTIPLICACIÓN
Ya hemos visto la suma y la resta con números decimales. En este apartado vamos a aprender la multiplicación de números decimales. La multiplicación de decimales es un poco diferente a la suma y la resta de decimales.
En la multiplicación con decimales colocamos los números en columnas, como si fuesen números naturales, sin tener en cuenta la coma, y resolvemos la multiplicación. A continuación, colocamos la coma en el resultado según el número de cifras decimales que componen los números decimales multiplicados. Veamos un ejemplo para que quede más claro.
En el ejemplo se va a multiplicar 42,43 por 1,2. Los colocamos como si no fuesen números decimales, quitándoles la coma, por lo que quedaría 4243 por 12. Cuando realicemos la multiplicación y tengamos el resultado, en este caso 50916 llega el momento de colocar la coma. El número 42,43 tiene 2 decimales y el número 1,2 tiene 1 decimal. En total 3 decimales. Por lo que el resultado final tiene 3 decimales, por lo que la coma se colocaría en el tercer lugar empezando por la derecha. El resultado final es 50,916.
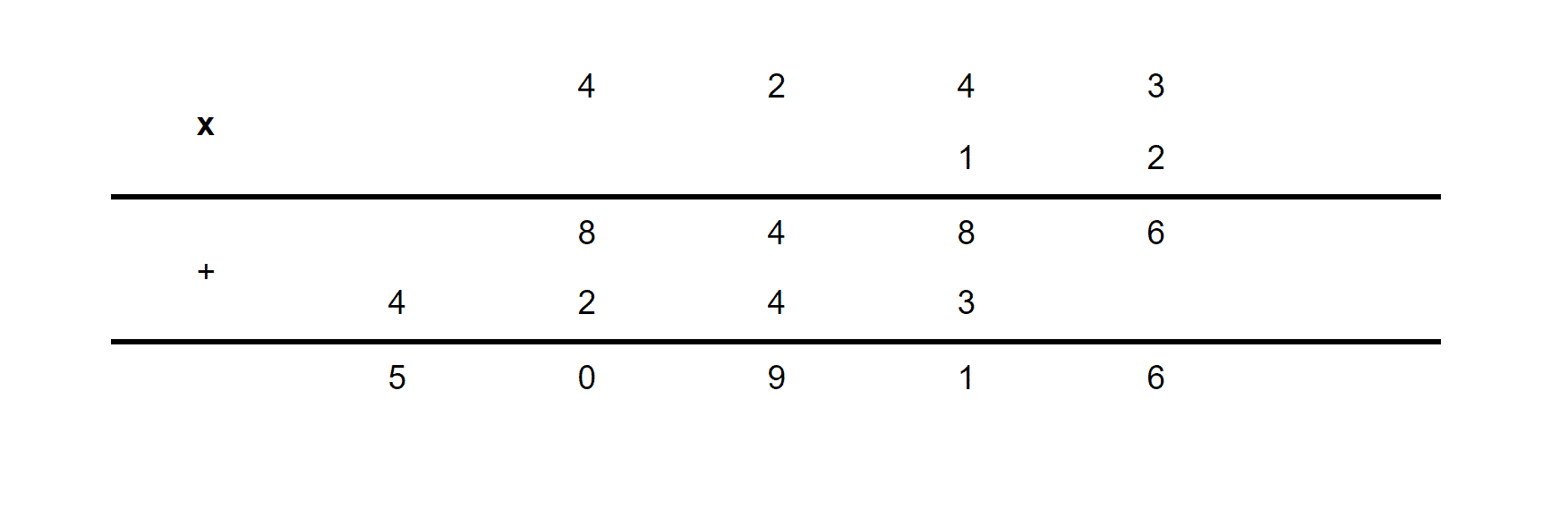
COMPARACIÓN
En algunos casos, será necesario comparar un número decimal con otro, por ejemplo, para saber cual de ellos es mayor o menor.
- Hay que empezar comparando la parte entera de ambos números decimales. El que tenga la mayor parte entera será el número decimal mayor.
Por ejemplo: 4,55 es mayor que 3,23, ya que 4 es mayor que 3.
- Si las partes enteras son iguales, se compara la parte decimal, empezando por las décimas.
- Si las décimas son iguales, se compara las centésimas, y se comprueba cual es mayor.
- Y finalmente, si las unidades, las décimas y las centésimas han resultado iguales, habría que comparar las milésimas, para determinar qué número es mayor.
Veamos un ejemplo para entenderlo mejor.

En el ejemplo de la imagen tenemos tres números decimales: 1,85, 1,83 y 1,86. Empezamos comparando la parte entera. Los tres números tienen la misma cifra, 1. Por lo que tenemos que comparar la parte decimal, empezando por las décimas, y si es necesario, seguiremos comparando centésimas y por último milésimas. En este ejemplo, las décimas también son iguales, ya que tienen la misma cifra, 8. Por lo que, seguimos comparando y lo hacemos con las centésimas. Las centésimas tienen valor diferente, siendo el orden de menor a mayor: 3 < 5 < 6.
Por lo tanto el resultado es:
1,83 < 1,85 < 1,86
APROXIMACIÓN
En muchos casos se aproxima el número decimal a la unidad, es lo que se conoce como redondear. Es una forma más sencilla de mostrar el resultado cuando tenemos números decimales. Vamos a aprender cómo se redondea a la unidad y a la décima.
Para redondear a la unidad un número decimal hay que tener en cuenta dos sencillas reglas:
- Regla 1: Si la décima es menor de 5 se queda el valor de la unidad igual.
Por ejemplo: 7,2 se redondea a 7.
- Regla 2: Si la décima es igual o mayor a 5, se aproxima la unidad al valor superior.
Por ejemplo: 1,8, se redondea a 2.
Para redondear a la décima un número decimal, se realiza un proceso similar al anterior, y se tienen en cuenta las siguiente reglas:
- Regla 1: Si la centésima es menor a 5, se queda el valor de la décima igual.
Por ejemplo: 6,23 se redondea a 6,2
- Regla 2: Si la centésima es igual o mayor a 5, se aproxima la décima al valor superior.
Por ejemplo: 1,26 se redondea a 1,3
EJERCICIOS DE NÚMEROS DECIMALES CON SMILE AND LEARN
La plataforma educativa Smile and Learn cuenta con la isla de aprendizaje de lógica y matemáticas que incluye una categoría para los números. Es una aplicación segura para los niños, ya que no tiene publicidad, no permite el acceso a internet o redes sociales. Todo el contenido está creado por educadores y lo podéis encontrar en varios idiomas. En la plataforma educativa de Smile and Learn los niños de 3 a 12 años, pueden aprender lógica, matemáticas, ciencias, lengua, artes, emociones y muchas cosas más.
A continuación, puedes probar la actividad de “Decimales”, que está incluida en la plataforma educativa Smile and Learn haciendo clic en la imagen.
Si deseas probar el resto de juegos, vídeos y cuentos interactivos, descarga nuestra plataforma educativa con más de 5.000 recursos, puedes solicitar un usuario demo de Smile and Learn durante 30 días totalmente gratis y sin compromiso.
El contenido de la actividad de decimales permite seleccionar previamente una serie de opciones de juego. Por ejemplo, que los números decimales se muestren con coma o punto y la elección del idioma. Cuenta con un apartado llamado “Aprende” por si necesitas unas nociones previas para la realización de los diferentes ejercicios. Y además en cada actividad hay un breve tutorial explicativo.

A continuación te detallamos las actividades que puedes realizar dentro de la categoría de números decimales.
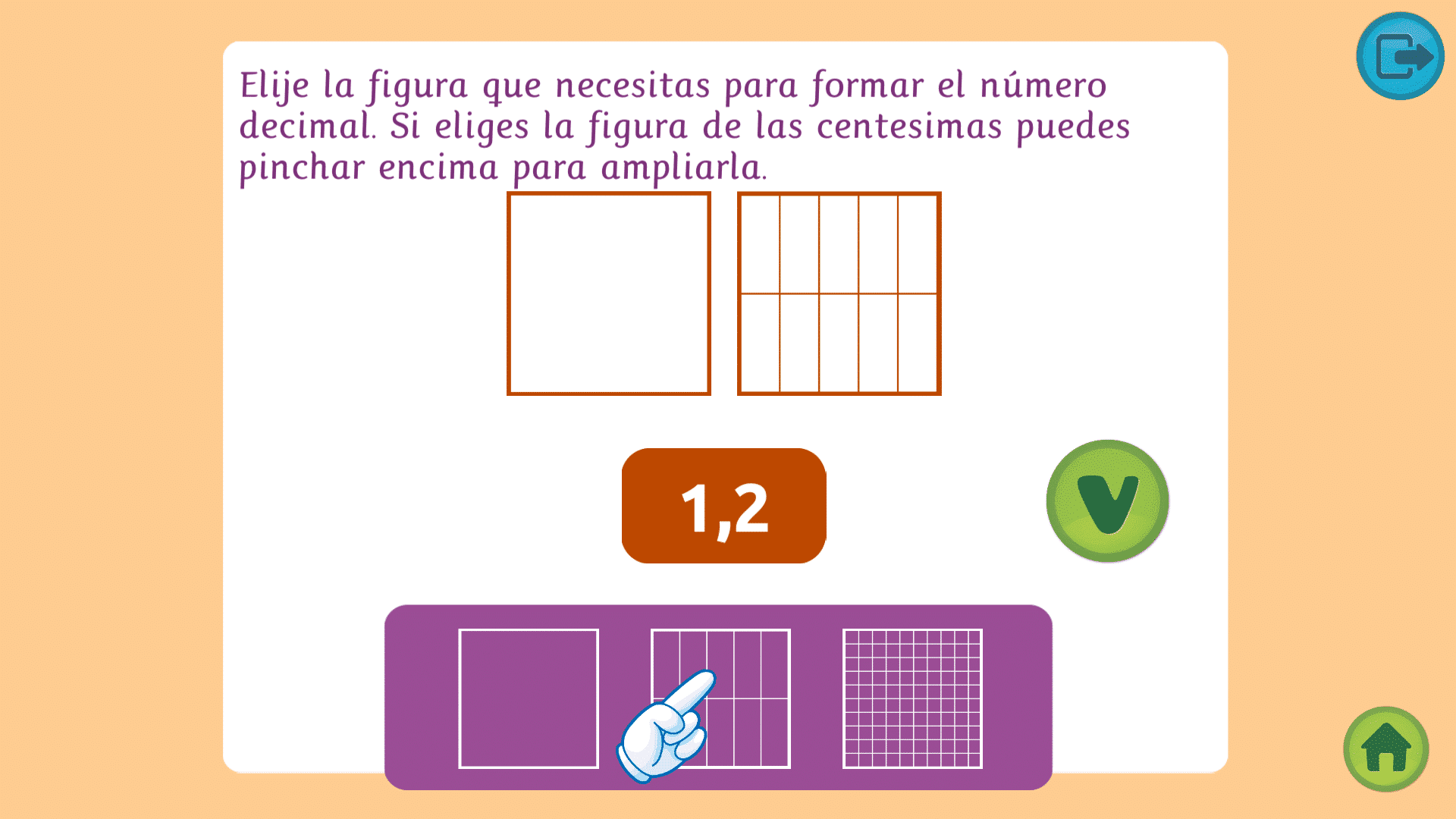
NÚMEROS DECIMALES EJERCICIOS: RELLENAR
En esta actividad el niño aprenderá a trabajar los números decimales con un ejercicio en el que deberá formar el número decimal eligiendo las figuras necesarias de unidad, décimas y/o centésimas.
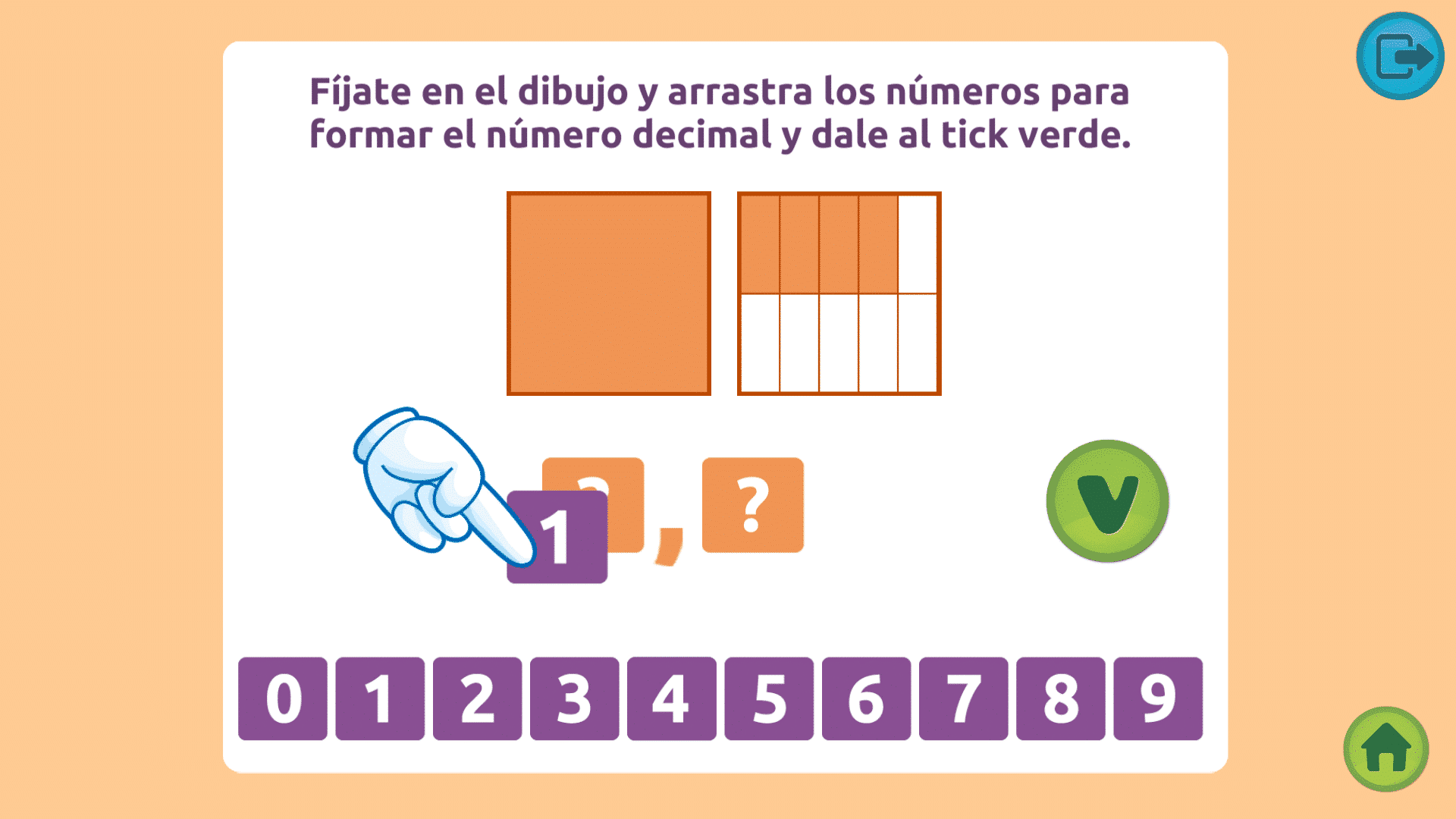
NÚMEROS DECIMALES EJERCICIOS: COMPLETAR
En este ejercicio se debe de indicar cual es el número decimal que aparece representado en los cuadrados de unidad, décimas y centésimas.
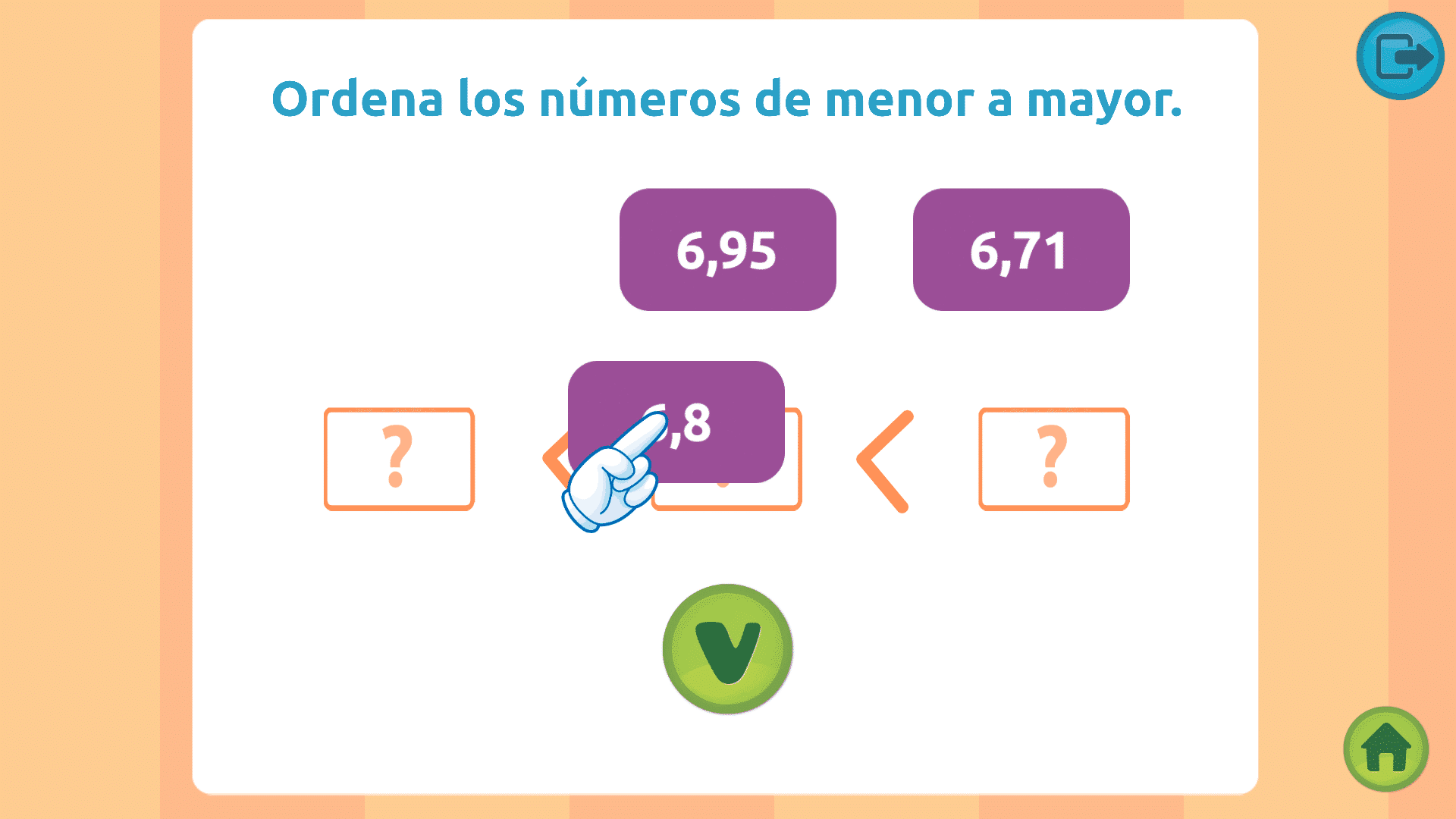
NÚMEROS DECIMALES EJERCICIOS: ORDENAR
Esta actividad pretende trabajar el orden de los números decimales. Para ello deberá de ordenar los números de mayor a menor, o viceversa, y colocarlos en la secuencia correcta.
Si os ha gustado la actividad de “Decimales” os recordamos que podéis probar nuestra plataforma educativa Smile and Learn solicitando un usuario demo de Smile and Learn, para probar de forma gratuita durante 30 días y sin compromiso las actividades, juegos y cuentos interactivos que contiene. ¡Os esperamos!